Devo ammettere che sono rimasto stupito dal numero di commenti all'articolo sugli sciami elettromagnetici. Ma come? Meno di una decina di tentativi di risposte al compito a casa? Non che me aspettassi migliaia, ma visto che quell'articolo negli ultimi giorni è stato letto (o perlomeno aperto) parecchie centinaia di volte, il rapporto tra letture e tentativi di risposta mi sembra un po' scarso. Forse l'articolo era troppo lungo, e non tutti sono arrivati al fondo (TL;DR?). O forse alcune delle mie ipotesi di fondo erano sbagliate.
Nella mia visione rosea del mondo, il calcoletto proposto nei compiti a casa doveva infatti essere alla portata di uno studente delle superiori. Forse la mia immagine dello studente medio delle superiore è appunto un po' troppo rosea, sia in termini di competenze specifiche (invertire un esponenziale? Fare un logaritmo?), sia, ed forse è peggio, i termini di capacità di ragionamento analitico. Riflettendoci un po', questo è forse il problema principale della divulgazione scientifica. Che cosa interessa della scienza? Le immagini mirabolante? L'impressione di aver capito? Però - non sia mai - senza fare un conto! Come se i conti fosse accessori alla comprensione, anche quella semplificata, un orpello necessario al tecnico che ci lavora per davvero, ma non a chi vuole solo capirne un po'. Beh, non credo sia vero, e proverò a dimostrarvelo proprio con l'esempio del calorimetro elettromagnetico di cui abbiamo parlato.
Il compito a casa chiedeva di calcolare quante lunghezze di radiazione servono a fermare in fotone (o un elettrone) con energia di 100 GeV o 1 TeV nell'ipotesi semplificatissima che l'energia critica sotto la quale le particelle di uno sciame elettromagnetico vengono assorbite dal materiale che attraversa sia 10 MeV, e che per ogni lunghezza di radiazione attraversata ogni particella dello sciame si sdoppi in due particelle con metà dell'energia. Come si risolve questo problema? Ci sono diversi approcci possibili, più o meno formali.
Iniziamo con quello intuitivo, probabilmente più semplice. Il fotone iniziare ha energia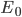 
, e produce uno sciame con 
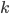particelle, ognuna delle quali avrà energia 
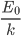. Quando questa energia è uguale (o minore) dell'energia critica di 
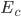= 10 MeV, allora lo sciame si ferma. Posso calcolare al volo quante particelle deve avere lo sciame per fermarsi: 
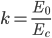, ovvero 
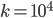nel caso 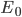= 100 GeV (1 GeV sono 
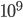eV, 1 MeV 
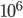eV), 
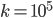per 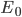= 1 TeV (1 TeV = 
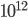eV) (se siete persi nei suffissi scientifici mega, giga e tera, data un'occhiata qui). Quante lunghezze di radiazione mi servono perché la mia particella iniziale si trasformi in uno sciame di 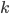particelle? Se il numero di particelle raddoppia ogni lunghezza di radiazione attraversata, dopo un numero 
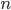di lunghezze di radiazione avrò 
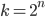particelle. Potete mettervi pazientemente con carta e penna o una calcolatrice, e trovare qual è la potenza di 2 che approssima di più 
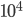e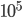 
. Per i pigri, sono rispettivamente un po' meno di 14 (
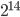= 16384) e un po' meno di 17 (
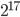= 131072).
Ma un fisico (o lo studente delle superiori dei miei sogni) non risolverebbe così il problema! Troppi passaggi, e il prova-e-riprova con la calcolatrice è lungo e inefficiente. Meglio un approccio più formale, e un paio di formulette. Pronti? L'energia di una particella nello sciame semplificato che stiamo descrivendo è:
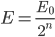
dove 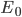è l'energia iniziale del fotone, e 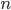il numero di lunghezze di radiazione attraversate. Lo sciame si ferma quando 
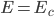, e dunque:
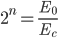
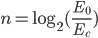
dove il secondo passaggio dovrebbe esservi chiaro se avete studiato i logaritmi, cosa che, se fanno fede le mie ricerche, si dovrebbero ancora studiare al terz'anno del liceo scientifico, e a un livello simile negli istituti tecnici (sul liceo classico non mi pronuncio!). Altrettanto semplice dovrebbe essere la trasformazione in logaritmo in base 10 (perché non tutte le calcolatrici sanno calcolare i logaritmi in base 2). Se infatti andate a rinvangare nel vostro libro di matematica delle superiori, troverete questa formula:
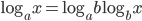
che ci permette di riscrivere:
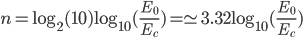
Con questa formula potete risolvere al volo il problema che vi ho dato: per 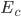= 10 MeV, 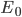= 100 GeV o 1 TeV, al volo trovate 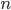= 13.28 o 16.61. Che tra l'altro, è un risultato esatto rispetto alle approssimazioni fatte prima.
Ma la cosa migliore è che questa formula vi permette di risolvere il problema per tutte le situazioni possibili: per qualunque energia del fotone o dell'elettrone entrante, e per qualunque valore dell'energia critica sotto la quale le particelle dello sciame vengono assorbite (che può dipendere dal materiale che sceglierete). Questo vi permette per esempio di fare un grafico del genere, dove disegnare, per un certo valore dell'energia critica, quante lunghezze di radiazione vi servono per fermare un fotone in funzione della sua energia iniziale:
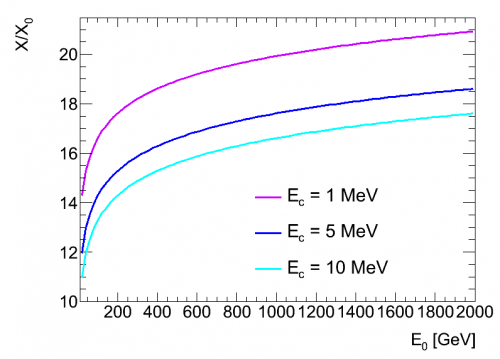
Un'occhiata a questo grafico vi insegna molte più cose che mille parole: per esempio, che la quantità di lunghezze di radiazione necessarie per fermare un fotone non cresce in modo costante con l'energia del fotone stesso. Se raddoppia l'energia del fotone, non avete bisogno di raddoppiare la lunghezza del vostro rivelatore per fermarlo. La cosa è vantaggiosa, perché invece, per misurare con precisione una particella con tracciatore, la dimensione di questo rivelatore dovrebbe crescere in modo linearmente proporzionale con l'energia. Un grafico come quello lì sopra vi permette di fare non solo delle previsioni puntuali (quante lunghezze di radiazione per fermare una particella di una certa energia), ma anche di comprendere delle proprietà globali (la lunghezza necessaria non aumenta linearmente con l'energia, dunque questo tipo di rivelatore potrebbe rivelarsi più appropriato, rispetto a un tracciatore, per particele di alta energia).
Questo è il segreto principale del successo indiscusso della modelizzazione matematica dei fenomeni naturali: certo, da una parte il poter calcolare in modo puntuale le caratteristiche di un certo fenomeno in determinate condizioni. Ma anche - soprattutto! - il poterne cogliere le proprietà globali, le sole che permettono una comprensione profonda non solo del funzionamento, ma anche del senso di un fenomeno, e del suo ruolo in un contesto più ampio. Non abbiatene paura!
© Marco @ Borborigmi di un fisico renitente, 01/03/2012. (Some right reserved)|
Permalink |
31 commenti
Archiviato in Fisica, Scienza e dintorni| Tag: divulgazione, formulette, logaritmo, matematica, rivelatori, sciame elettromagnetico