Supponiamo siate un fisico delle particelle, un fisico sperimentale, per essere precisi. Supponiamo che lavoriate a un esperimento che sta seduto su un acceleratore; un collisore, per essere precisi, come Tevatron, o LHC. Supponiamo siate interessati alla ricerca di una qualche particella esotica, uno dei mattoncini mancanti della vostra teoria preferita; il bosone di Higgs del Modello Standard, tanto per fare un esempio a caso. Come fate a sapere quante di queste particelle esotiche di cui siete alla ricerca - se esistono - vengono prodotte nelle collisioni gentilmente offerte dal vostro acceleratore?
Per rispondere a questa domanda vi servono fondamentalmente quattro ingredienti: una stima decente di quella che si chiama la luminosità del collisore; un amico teorico che vi aiuti a calcolare la sezione d'urto di produzione della particella che state avidamente cercando, per le energie tipiche delle vostre collisioni; una certa abilità a fare equivalenze e moltiplicazioni in notazione esponenziale; e questa semplice formuletta:
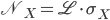
Formuletta che, tradotta dal matematico al fisichese, recita: il numero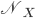 
di particelle 
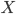prodotte nell'unità di tempo (ovvero per secondo) al mio collisore di fiducia è pari alla luminosità istantanea 
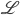del suddetto collisore, moltiplicata per la sezione d'urto di produzione 
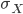della particella 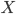, calcolata per l'energia nel centro di massa delle collisioni in questione. Vediamo di spiegare che cosa sono i due ingredienti della formula.
Luminosità
La luminosità istantanea 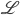mi dice quante particelle il mio acceleratore fa passare per il centro del mio rivelatore per unità di tempo. Tradizionalmente la luminosità istantanea si misura in 
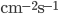: si tratta dunque della misura del numero di particelle che attraversano un'unità di area (un centimetro quadrato) in un secondo. Se voglio sapere quante particelle sono passate in un certo lasso di tempo dovrò calcolare la luminosità integrata 
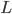: supponendo che la luminosità istantanea sia constante, basterà che moltiplichi quest'ultima per l'intervallo di tempo in questione, per ottenere qualcosa che avrà la dimensione di un numero per unità di area (
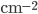). Esempio: se e quando LHC raggiungerà la sua "alta" luminosità nominale (
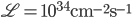), in un giorno di attività (24 h 
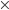60 m/h 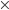60 s/m = 86400 s) accumulerà una luminosità integrata:
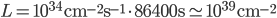
Siccome a noi fisici piacciono le unità di misura bizzarre, ne usiamo una speciale per le unità di area con cui abbiamo a che fare, il barn:
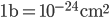
La storia del nome barn, che in inglese vuol dire granario (o magazzino), sarebbe interessante da raccontare, ma tralasciamo. La luminosità integrata in un giorno di LHC che lavori senza pause ad "alta luminosità" sarebbe dunque:
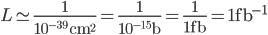
ovvero "1 femtobarn inverso". Può darsi che adesso le informazioni dei giorni scorsi inizino a sembrarvi più chiare, chissà. Per chi a questo punto si fosse perso nelle conversioni, consiglio un passaggio da queste parti prima di proseguire.
Sezione d'urto
Qui entriamo in territorio spinoso. Iniziamo dalle unità di misura: la sezione d'urto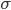 
è qualche cosa che ha la dimensione di un'area, e che dunque potremmo misurare in 
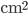, ma che normalmente, visto che si tratta sempre di aree molto piccole, misuriamo in (frazioni di) barn. Cercando di dirla in parole semplici, la sezione d'urto esprime la probabilità che un certo tipo di processo abbia luogo. Perché dunque un'area? Prendiamo il caso di un evento "semplice": prima ancora di parlare di produzione di particelle, esaminiamo la generica "collisione" di due protoni. Se tentate (come cercheremo di fare a LHC) di far sbattere l'uno contro l'altro due protoni, e se immaginate che i due protoni siano due sferette, è facile intuire che la collisione avrà luogo solo se l'asse del moto del primo sarà compreso in un'area parti a una circonferenza di raggio doppio del raggio del protone, centrata intorno al secondo protone:
Per capire lo schema: i dischi marroni sono i protoni; quelli con le crocette gialle viaggiano verso l'interno delle schermo, quello senza crocette viene dallo schermo verso di voi. Nella realtà le cose sono ben più complicate (e i protoni non sono affatto sferette!), ma l'esempio serve a dare un'idea, e i numeri che ne escono sono ragionevoli:
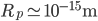
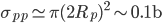
Quest'area rappresenta (una ragionevole approssimazione del-) la sezione d'urto totale di interazione protone-protone a LHC. Questa è la quantità che dovete confrontare con la misura del flusso di particelle per unità di area nel tempo (la luminosità integrata) per sapere quante interazioni protone-protone avranno luogo. Tornando all'esempio di prima, in un giorno di LHC ad alta luminosità a 14 TeV ci saranno dunque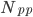 
interazioni:
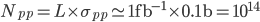
Naturalmente non tutte queste interazioni sono interessanti, nel senso che non in tutte le collisioni viene scambiata sufficiente energia - la maggior parte sono collisioni "periferiche", in cui i due protoni si sfiorano appena - perché avvengano quei fenomeni interessanti da osservare, come la produzione della vostra particella esotica preferita. Questa è la ragione per cui ci servono acceleratori così luminosi: è l'unico modo per poter (tentare di) osservare fenomeni rari.
Per fare calcoli per questi fenomeni rari dobbiamo munirci di sezioni d'urto specifiche, che misurino per esempio la probabilità che la particella che ci interessa venga prodotta nelle interazioni generate dal nostro collisore. Queste sezioni d'urto, come la sezione d'urto di interazione totale, continuano ad essere misurate in unità di area, ma hanno ovviamente valori molto più piccoli. Come si calcolano? Non provate nemmeno a chiedermelo: è per questo che vi serve l'amico teorico!
Ecco invece un numerello per darvi un'idea: per un'energia nel centro di massa di 14 TeV la sezione d'urto di produzione del bosone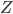 
vale circa 
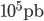. Fatevi il conto di quanti ne verranno prodotti in un giorno di LHC ad alta luminosità, e confrontatelo con quante interazioni "generiche" avvengono. Oppure confrontate direttamente le sezioni d'urto.
Compito a casa
Se crediamo alle previsioni del CERN, LHC partirà a fine anno, funzionerà per quasi tutto il 2010 (senza sosta e senza problemi), e fornirà come promesso agli esperimenti una luminosità integrata di circa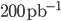 
a 10 TeV di energia nel centro di massa. Sapendo che la sezione d'urto (teorica) di produzione di un bosone di Higgs del Modello Standard in collisioni protone-protone a 10 TeV è 
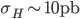(il valore cambia un po' in funzione della massa dell'Higgs, e soprattutto cambia in funzione del meccanismo di produzione, ma la stima che vi do per il meccanismo dominante rimane ragionevole per quello che ci serve), quanti bosoni di Higgs (se esistono, e se i calcoli dell'amico teorico sono corretti) verranno prodotti nel corso di tutto il run del 2009-2010? Sono tanti? Sono pochi?
Con la risposta in tasca, prima o poi vedremo di trovare il tempo di discutere del perché Tevatron possa restare competitivo ancora un po' nella ricerca dell'Higgs, e soprattutto del perchè pure con un numero apparentemente dignitoso di esemplari prodotti sia comunque difficile scoprire una nuova particella. Perché (indizio!) produrre una particella non significa affatto riuscire a vederla. Buoni calcoli.