Quando LHC andava ancora di moda, tra le tante richieste di spiegazione sganciate su queste pagine ce n'era una ricorrente: perché accelerate protoni, e non per esempio elettroni? In effetti gli elettroni sono più leggeri, ed essendo particelle veramente elementari (cioè non composte da altre particelle, per quel che ne sappiamo. I protoni invece sono composti da quark), sarebbe bello poterli usare in collisioni alle energie di LHC: sarebbe tutto molto più pulito, con meno "detriti" in giro ad ogni collisione, dunque con misure più facili e precise.
C'è però un impedimento non trascurabile, che si chiama radiazione di sincrotrone. Una particella carica che viaggi su una traiettoria circolare emette questo tipo di radiazione, emissione che comporta una perdita di energia. In regime relativistico, a ogni giro la particella in questione perde:
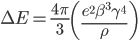
dove 
è la carica dell'elettrone (o del protone, è la stessa), 
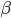la sua velocità (misurata in unità di velocità della luce nel vuoto, come abbiamo già discusso), e
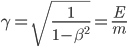
misura - tra le altre cose - il rapporto tra la massa della particella e la sua energia (anche per questo fattorello, se avete un minuto riguardatevi questo articolo).
Allora, adesso immaginate di prendere un elettrone e un protone, e di accelerarli fino a che abbiamo la stessa energia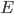 
. Immaginate di fare il tutto dentro lo stesso acceleratore, quindi con il medesimo raggio di curvatura 
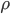: potete allora calcolare il rapporto tra le perdite di energia per radiazione di sincrotrone nei due casi (il bello di calcolare un rapporto è che potete buttare via un sacco di termini, grazie al fatto che 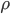ed 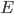sono gli stessi, e che il rapporto tra le velocità 
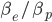è praticamente uguale a uno in un regime ultrarelativistico):
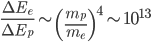
Ecco la cruda verità: a parità di energia un elettrone perderebbe diecimila miliardi di volte più energia per giro che un protone a causa della radiazione di sincrotrone. Che è la ragione per cui, volendo salire in energia usando lo stesso tunnel, dopo LEP (un acceleratore di elettroni e positroni) è stato costruito LHC (un acceleratore di protoni).
Avendo voluto continuare a collidere elettroni cone si faceva a LEP, ma a energia più alta, avremmo dovuto usare cavità acceleratrici veramente troppo potenti, o scavare un tunnel circolare dal diametro molto maggiore (cosa non esattamente agevole). Oppure optare per una geometria lineare, ed eliminare del tutto il problema della radiazione di sincrotrone, idea che in effetti sta dietro ai progetti per i potenziali successori di LHC.