Alla fine della puntata precedente scoprivamo che della lagrangiana del Modello Standard si dice spesso che è un' equazione che "riassume elegantemente la nostra conoscenza del mondo delle particelle elementari e delle loro interazioni fondamentali". Ci chiedevamo allora se questa fosse una frase accurata, e un particolare quanto fosse corretto l'uso della parola "conoscenza". Per provare a rispondere a queste domande, dobbiamo cominciare con il sezionare i termini della lagrangiana, provando a capire che cosa rappresentano e descrivono.
Disclaimer 1: questo non è, e non ha nessuna intenzione di essere, un corso di fisica teorica. In questo articolo e nei seguenti farò un uso molto approssimato e liberale delle equazioni, con l'unico scopo di indicarvi da molto lontano che cosa rappresentino i vari termini. Non aspettatevi nessuna spiegazione dettagliata della struttura matematica della teoria, né di come i vari pezzi sono usati per calcolare le proprietà che andiamo a misurare.
Disclaimer 2: per la lettura di questo articolo una certa conoscenza pregressa è data per scontata (per esempio, serve sapere quali sono le quattro interazioni fondamentali). Se non sapete di che cosa si sta parlando, seguite i link che disseminato nel testo: gli articoli di Wikipedia sono un buon punto di partenza per approfondire. E abbiate pazienza.
Partiamo dunque dalla lagrangiana del Modello Standard, nella versione compatta che vi mostravo nell'ultimo articolo. Ci concentreremo inizialmente sulle prime due righe:
Queste due righe sono la porzione della lagrangiana che descrive la struttura delle interazioni fondamentali, e come queste agiscono sulle particelle di materia. Delle quattro forze che agiscono nel nostro mondo, il Modello Standard descrive infatti l'interazione elettromagnetica, l'interazione (nucleare) debole e l'interazione (nucleare) forte. In quelle due righe si sono dunque condensate (molto condensate!) la struttura dell'interazione elettrodebole, che unifica elettromagnetismo e forze nucleare debole, e della quantocromodinamica, la teoria che descrive l'interazione nucleare forte come scambio di gluoni tra quark.
Iniziamo con il decrittare (a spanne!) i simboli. La prima riga:
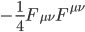
contiene la descrizione di come i campi delle interazioni descritte (elettrodebole o forte, qui rappresentate in modo generico: per loro descrizione dettagliata bisognerebbe studiare la versione estesa della lagrangiana) interagiscono tra di loro. Il simbolo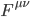 
nasconde il potenziale 
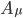dell'interazione in questione:
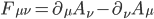
Discutere che cosa sia il "potenziale di un'interazione" richiederebbe un intero corso di fisica, limitiamoci dunque a dire che si tratta di un oggetto matematico da cui è possibile ricavare le proprietà del campo dell'interazione in questione. E che cos'è il campo di un'interazione? Eh, la fisica è come il tunnel di Alice... Diciamo solo che è un altro oggetto matematico che assegna un valore di una certa quantità (per esempio, semplificando molto, l'intensità di una certa interazione), a un punto dello spazio(-tempo). Gli apici e pedici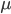 
e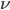 
rappresentano le dimensioni degli oggetti: siccome il Modello Standard è una teoria relativistica (nel senso della relatività ristretta), tutti gli oggetti hanno quattro dimensioni, una temporale e tre spaziali.
Intermezzo per i curiosi che masticano un po' di matematica. Gli apici e pedici 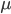e 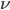non rappresentano solo le dimensioni, ma anche, a seconda di come sono messi e se sono ripetuti, operazioni di somma sui medesimi indici. Il simbolo 
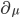è un modo compatto per indicare una derivata parziale rispetto alla dimensione indicata dall'indice.
Intermezzo per i curiosi che masticano un po' di fisica classica. Saltando allegramente tra formulazione classica e quantistica, diciamo che 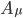è un quadrivettore che, nel caso dell'interazione elettromagnetica che prendiamo come esempio, può essere definito come:
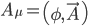
dove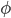 
è il potenziale scalare e 
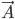il potenziale vettoriale dell'interazione elettromagnetica nella sua formulazione relativistica, da cui posso ritrovare le buone vecchie equazioni di Maxwell (nella forma tensoriale relativistica):
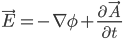
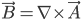
Intermezzo per i pignoli che sanno di cosa parlo. Lo so, lo so, la forma reale di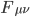 
per le interazioni debole e forte è un dito più complessa, perché contiene anche un termine che descrive la mutua interazioni dei bosoni tra di loro, che siano i bosoni 
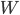e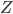 
dell'interazione debole o i gluoni della QCD. Come dicevo, questo non è un corso di fisica teoria.
(Fine degli intermezzi pignoletti)
La seconda riga descrive come i campi delle interazioni interagiscono con i campi che rappresentano le particelle di materia:
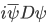
La lettera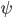 
rappresenta il campo associato a una particella di materia, per esempio un elettrone o un quark. L'interazione è invece nascosta dietro al quella lettera D sbarrata. Il primo a usare questa "notazione con la sbarra" fu Dirac, anche se i fisici la conoscono normalmente come notazione sbarrata di Feynman. Con un unico simbolo, per amor di brevità si indica il prodotto tra un vettore (per i pignoli: un vettore covariante) e le matrici di Dirac (o matrici gamma);
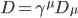
Non entreremo nella questione di che cosa siano le matrici di Dirac, diciamo solo che la notazione sbarrata serve a nasconderle per rendere la scrittura più compatta. Che cos'è invece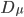 
? È quella che in gergo si chiama derivata covariante, una versione sofisticata della derivata che magari ricordate dalle superiori, che ha però altre proprietà interessanti, tra cui quella di mantenere le proprietà di simmetria dell'oggetto a cui viene applicata:
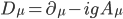
Dentro al termine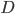 
è dunque nascosto il campo dell'interazione in questione 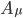(per esempio il campo elettromagnetico), mentre 
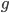è quella che chiamiamo costante di accoppiamento dell'interazione, un numero che definisce quanto intensamente agisce la forza in questione.
La storia di questo pezzo della lagrangiana del Modello Standard è molto lunga. Comincia con l'elettrodinamica quantistica di Feynman, che a sua volta è il culmine di un lavoro che parte da Dirac e passa per Fermi e Bethe, solo per citare alcuni dei contributori più importanti. Continua con la sua estensione all'interazione debole, e all'unificazione di quest'ultima con l'interazione elettromagnetica da parte di Glashow, Salaam e Weinberg, vero fondamento del Modello Standard. E culmina con la formulazione della cromodinamica quantistica, e con la scoperta della libertà asintotica.
Le equazioni che abbiamo provato a sviscerare sono spesso rappresentate sotto forma di diagrammi di Feynman. Per quanto questi siano in primo luogo un modo che i fisici hanno per organizzare i calcoli, possono essere utili per visualizzare i processi che i calcoli rappresentano. Ecco i diagrammi che quelle equazioni rappresentano, al loro livello di sviluppo più semplice:
Per queste prime due righe della lagrangiana del Modello Standard, possiamo dunque parlare di "conoscenza" nel suo senso più completo. Si tratta del condensato di quella fisica che per certi versi inizia con la stesse equazioni di Maxwell nel 1880, e la cui struttura e proprietà abbiamo testato e misurato con altissima precisione nel corso di tutto il novecento. Che dire invece delle altre due righe?
(continua)