Secondo articoletto della categoria Formulette (e pazienza per la radiazione di sincrotrone che avevo promesso: sarà per un'altra volta). Oggi vi propongo di giocare un po' con la formula di fisica più famosa del mondo. Che - credo sarete d'accordo - è senza dubbio questa:
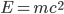
La si trova dappertutto (insieme al faccione irriverente dell'Einstein degli ultimi anni), simbolo dei trionfi (e anche dei disastri, se pensate all'energia nucleare) della fisica moderna del 900.Cosa dice questa formula? Ci rivela la geniale scoperta di Einstein: un corpo di massa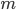 
a riposo è un incredibile serbatoio di energia 
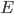, che può essere calcolata come il prodotto della sua massa 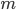per il quadrato della velocità della luce 
.
Quello che è un peccato è che la formula più famosa del mondo - così come è scritta lassù - ha almeno due difetti. Primo, vale solo per corpi a riposo: appena ci si sposta in un sistema di riferimento in cui il corpo in questione si muove, beh, non vale più (tra un minuto vediamo perché questo è un bel limite alla comprensione); la formula generale, quella che vale per un corpo qualunque sia la sua velocità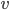 
, è questa:
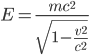
che è di certo meno facile da mettere sulle magliette o negli spot pubblicitari. Secondo, usa delle unità di misura innaturali, che aggiungono una complicazione probabilmente inutile alla formula, e, di nuovo, alla comprensione.
Iniziamo dalle unità di misura. La relatività speciale di Einstein ci dice che nulla si può muovere a una velocità maggiore di quella della luce . A pensarci bene, se esiste una velocità limite, allora sarebbe sensato misurare ogni velocità in termini di questa velocità massima. Avrebbe molto più senso (perlomeno quando si fa fisica, forse non in autostrada) dire che un corpo viaggia a un centesimo della velocità della luce, piuttosto che a 3000 chilometri al secondo. Se decidiamo di usare questa convenzione (come tutti i fisici delle particelle fanno), possiamo ribattezzare la velocità come:
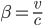
Se un corpo viaggia alla velocità della luce, avrà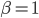 
. Se va a 3000 chilometri al secondo, avrà 
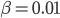. E naturalmente misurare le velocità in unità di equivale a dire che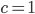 
, per cui la nostra formula iniziale (quella che vale per tutte le velocità) diventa:
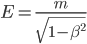
Un po' più semplice, no? Siccome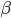 
non ha dimensioni (nel senso che è un numero puro, senza unità di misura), il trucchetto ci permette di misurare le masse e le energie (e i momenti, come vedremo tra un attimo) nella stessa unità di misura (scegliete voi quelle che vi piacciono: ai fisici delle particelle piacciono gli elettronvolt). Adesso facciamo un po' di magia con l'algebra (ce la potete fare!). In relatività il momento di un corpo si calcola come 
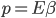, per cui se manipolate un po' l'ultima formuletta (fate il quadrato, moltiplicate a destra e sinistra per 
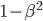, ...) potete ottenere questa qui:
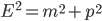
che, detto tra noi, dovrebbe prendere il posto di formula più famosa del mondo!
E adesso, non sentite un formicolio dietro alle orecchie? Sono sicuro di si! Cosa vi ricorda l'ultima formula che abbiamo scritto? Dai, un piccolo sforzo... ma certo: il teorema di Pitagora! Eh si, possiamo scrivere la formula più importante della relatività ristretta come fosse il teorema di Pitagora. Ganzo! Provate a dirlo ad alta voce: il quadrato dell'energia di un corpo è uguale alla somma dei quadrati della sua massa e del suo momento.
Che cosa possiamo imparare da questa filastrocca? Guardate questa figura:
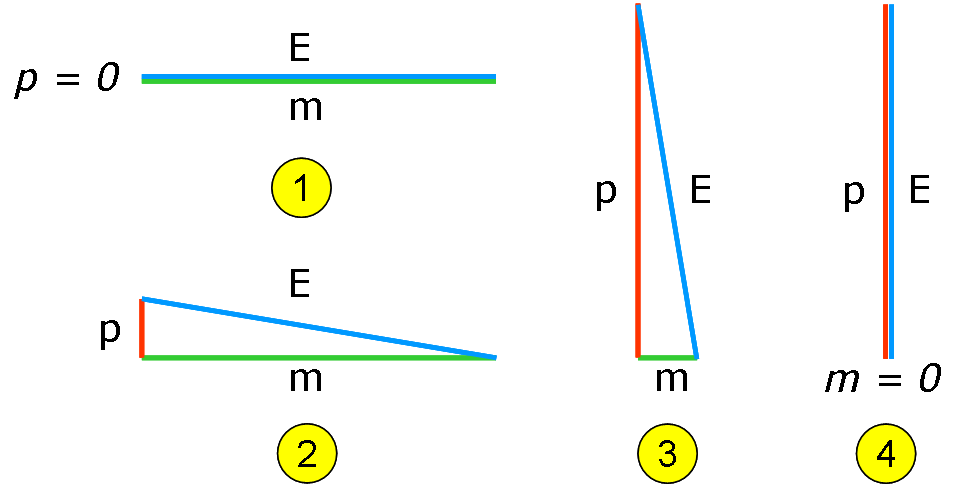
Nel caso (1) il corpo è fermo: la sua energia è completamente determinata dalla sua massa. Se il corpo in questione si muove (per esempio si tratta di Oliver che va a spasso) ha un momento molto più piccolo della sua massa (2), e la sua energia è ancora quasi completamente determinata dalla sua massa solamente. E' il caso dei movimenti di tutti i giorni, della fisica classica: piccole velocità e grandi masse. Ma se il momento della particella è molto più grande della sua massa (2) come nel caso delle particelle negli acceleratori (che sono leggere, almeno rispetto a Oliver) che viaggiano a velocità prossime a quelle della luce, beh, l'energia della particella è praticamente tutta determinata dalla sua velocità! E nel caso estremo di particelle senza massa (4) come il fotone, beh, queste viaggiano sempre... alla velocità della luce.
Adesso provate a usare questa figura per capire che cosa succede in un acceleratore di particelle. Prendete due particelle leggerine (diciamo sue protoni, come in LHC) e acceleratele a velocità prossime a quella della luce: siete nella condizione (3). Poi le fare sbattere l'una contro l'altra, e, come già sapete, avete a disposizione nello scontro la somma delle energie. Ovvero un'ipotenusa blu bella lunga. Adesso immaginate che nello scontro saltiate dalla condizione (3) a quella (2) (o anche (1), se volete): con l'energia a disposizione potete produrre particelle moooolto più pesanti (con un cateto verde molto più lungo), ma che si muovono decisamente più piano (un cateto rosso più corto). Questo è quello che fanno i collisionatori: trasformano energia cinetica (che è facile accumulare, accelerando particelle leggere) in massa. Producendo particelle più pesanti di quelle di partenza! E, naturalmente, potreste farlo anche saltando da (4) a (2), usando due fotoni energetici per produrre particelle massive. Non è forte?
Un grazie a L.B Okun a cui ho preso in prestito l'idea del teorena di Pitagora. Questo articoletto é un regalo per Anna, che si sbatte per poter insegnare la fisica (moderna e non) alle scuole superiori.